1937. Fire safety
In city X, there
are n houses. Some of them are
connected by one-way roads.
Recently, the
number of fires in city X has increased. To address this problem, the residents
decided to build several fire stations in the city. However, a difficulty
arose: when responding to an emergency, a fire truck may ignore the direction
of the roads, but on the way back it must strictly follow all traffic rules
(the residents of city X observe them rigorously!).
It is necessary
to ensure that, regardless of its current location, a fire truck can always
return to the same fire station from which it departed. Since building fire
stations is costly, the city council decided to construct the minimum possible
number of stations that satisfy this condition. In addition, in order to reduce
costs, fire stations may only be built next to existing houses.
Write a program
that determines the optimal placement of fire stations.
Input. The first line contains the
number of houses n (1 ≤ n ≤ 3000).
The second line contains the number of roads m (1 ≤ m
≤ 105).
Each of the following lines describes a road in the format ai bi, which means
that it is possible to travel along the i-th
road from house ai to house bi (1 ≤ ai, bi ≤ n).
Output. In the first line, print
the minimum number k of fire stations
that need to be built. In the second line, print k integers in any order – the indices of the houses next to which
the fire stations should be built.
If there are
multiple optimal solutions, print any of them.
|
Sample
input |
Sample
output |
571 22 33 12 12 33 4
2 5 |
2 4 5 |
SOLUTION
graphs – strongly
connected components
Algorithm analysis
The problem
requires finding a minimum set of vertices of the graph that is reachable from
all other vertices. To do this, we consider the condensation of the graph. Let
us focus on the strongly connected components from which no edges leave.
If a fire
station is not built in such a component, a fire truck arriving from another
component will be able to extinguish the fire, but it will not be able to
return back while following the directions of the roads. Therefore, in each
strongly connected component with no outgoing edges, at least one fire station
must be built.
There is no need
to build additional stations, since from any vertex of the graph there exists a
path along the edges to one of the components with no outgoing edges.
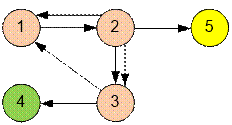
Example
The input graph contains
three strongly connected components. From the components consisting of a single
vertex (4 and 5), no edges leave. Therefore, it is sufficient to build fire
stations exactly in these components.
Algorithm implementation
Store the input graph in
the adjacency list g. The reversed graph (the graph in which the
directions of all edges are inverted) is stored in the adjacency list gr.
vector<vector<int> > g, gr;
vector<int> used, top, color, repr;
The function dfs1 implements
a depth-first search on the input graph. The array top stores the order
of vertices corresponding to the moments when their processing is finished
during the depth-first traversal.
void dfs1(int v)
{
used[v] = 1;
for (int to : g[v])
if (!used[to]) dfs1(to);
top.push_back(v);
}
The function dfs2 implements a depth-first search on the reversed graph. All
vertices visited as a result of recursive calls to dfs2
belong to the same strongly connected component. All such vertices are colored
with color c. Vertices that are in the same strongly connected component
have the same color.
For each color c, the array repr stores a
representative of the corresponding component – any
vertex number colored with this color.
void dfs2(int v, int c)
{
color[v] = c;
repr[c] = v;
for (int to : gr[v])
if (color[to] == -1) dfs2(to, c);
}
The main part of the program. Read the input data and
build the reversed graph.
scanf("%d %d", &n, &m);
g.resize(n + 1);
gr.resize(n + 1);
for (i = 0; i < m; i++)
{
scanf("%d
%d", &a, &b);
g[a].push_back(b);
gr[b].push_back(a);
}
Run a depth-first search on the original graph. The order
in which the processing of vertices is completed is stored in the array top.
used.resize(n+1);
for (i = 1; i <= n; i++)
if (!used[i])
dfs1(i);
Run a depth-first search on the reversed graph. The
vertices of the reversed graph are processed in the order given by the array top,
while the traversal is performed from right to left – from the end of the array
to the beginning. For convenience of further processing, the array top
is reversed beforehand.
color.assign(n+1, -1);
repr.assign(n+1, -1);
reverse(top.begin(),
top.end());
Vertices belonging to the same strongly connected
component are colored with the same color. The current color is stored in the
variable c.
c = 0;
for (int v : top)
if (color[v] == -1) dfs2(v, c++);
The variable c stores the number of strongly
connected components.
used.assign(c, 1);
for (i = 1; i < g.size(); i++)
for (int to : g[i])
Iterate over all edges of the graph (i, to) and check whether
the vertices i and to belong to different
strongly connected components. This is determined by their different colors. If
the vertices are in different components, then there is no need to build a fire
station in the component with color color[i], so we set used[color[i]]
= 0.
if (color[i]
!= color[to]) used[color[i]] = 0;
}
Count the number of components c where a fire
station should be built.
c = 0;
for (i = 0; i < used.size(); i++)
if (used[i])
c++;
Print the minimum required number of fire stations.
printf("%d\n",c);
For each component with color i from which no edges
leave, print its representative (the value repr[i]). These are exactly
the house numbers near which fire stations should be built.
for (i = 0; i < used.size(); i++)
if (used[i])
printf("%d ",repr[i]);
printf("\n");